Non-Deterministic Finite Automata
Dari sebuah mesin Non-Deterministic Finite Automata (NFA) dapat dibuat mesin Deterministic Finite Automata (DFA) yang ekuivalen/bersesuaian. Ekuivalen di sini artinya mampu menerima bahasa yang sama.
Sebagai contoh, akan dibuat Deterministic Finite Automata dari Non-Deterministic Finite Automata berikut:
Adapun langkah-langkahnya adalah sebagai berikut.
- Buatlah tabel transisi dari diagram transisi di atas.
-
Buatlah diagram transisi untuk finite state automata dari tabel transisi di atas. a. Kita mulai dari state awal yaitu q 0 b. Selanjutnya, kita telusuri lebih lanjut tentang q 0 , yaitu: c. Selanjutnya kita telusuri untuk state q1 , yaitu : Bila state q 1 mendapat input 0 maka menjadi state Ø Bila state q 1 mendapat input 1 maka menjadi state {q 0 ,q1 }, sehingga diperoleh gbr
d. Selanjutnya kita telusuri untuk state {q0 ,q1 }, yang merupakan penggabungan dari state q 0 dan state q 1 , sehingga hasil state {q0 ,q1 } merupakan penggabungan dari hasil state q 0 dan state q1 . Bila state q 0 mendapat input 0 menjadi state {q 0 ,q1 } Bila state q 1 mendapat input 0 maka menjadi state Ø Sehingga diperoleh jika state {q 0 ,q1 } mendapat input 0 menjadi state {q 0 ,q1 } Bila state q 0 mendapat input 1 menjadi state {q1 } Bila state q 1 mendapat input 1 maka menjadi state {q 0 ,q1 } Sehingga diperoleh jika state {q 0 ,q1 } mendapat input 0 menjadi state {q 0 ,q1 } Maka diagram transisi menjadi : e. Selanjutnya kita telusuri state Ø, yaitu : Bila state Ø mendapat input 0 dan 1 maka tetap menghasilkan Ø Sehingga diperoleh diagram transisi berikut f. tentukan finish state
Latihan
Buatlah DFA yang ekivalen dengan NFA berikut ini:
Soal Nomor 1
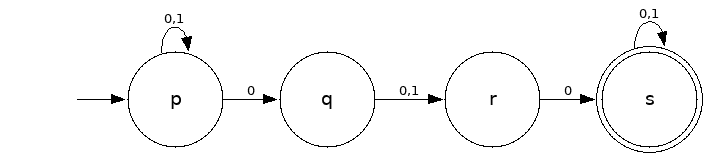
Q = {p,q,r,s}
Σ = {0,1}
S = p
F = {s}
| δ | 0 | 1 |
|---|---|---|
| p | {p,q} | {p} |
| q | {r} | {r} |
| r | {s} | Ø |
| s | {s} | {s} |
Soal Nomor 2
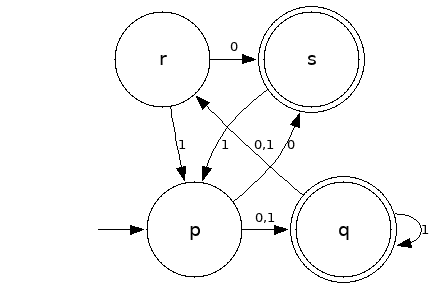
Q = {p,q,r,s}
Σ = {0,1}
S = p
F = {q,s}
| δ | 0 | 1 |
|---|---|---|
| p | {q,s} | {q} |
| q | {r} | {q,r} |
| r | {s} | {p} |
| s | Ø | {p} |
Soal Nomor 3
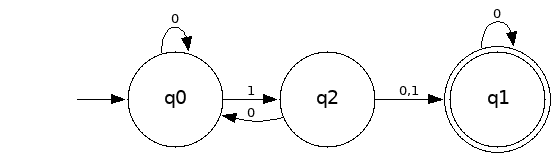
Q = {q0,q1,q2}
Σ = {0,1}
S = q0
F = {q1}
| δ | 0 | 1 |
|---|---|---|
| q0 | {q0} | {q2} |
| q1 | {q1} | Ø |
| q2 | {q0,q1} | {q1} |
Soal Nomor 4
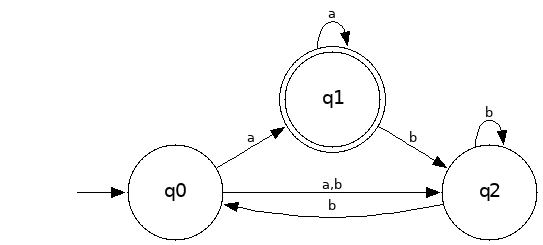
Q = {q0,q1,q2}
Σ = {a,b}
S = q0
F = {q1}
| δ | a | b |
|---|---|---|
| q0 | {q1,q2} | {q2} |
| q1 | {q1} | {q2} |
| q2 | Ø | {q0,q2} |